最終更新日: 2024年 4月 1日

Research / 研究

目次

研究概要

研究課題

偏微分方程式に関する逆問題

キーワード

ワードクラウド

論文紹介（要約とコメント付き）

偏微分方程式に関する逆問題

  1. Atsushi Kawamoto and Masahiro Yamamoto, Determination of an electromagnetic potential for the Dirac equation, Inverse Problems 28 (2012) 115012 (26pp).
    DOI : 10.1088/0266-5611/28/11/115012
    静電場におけるディラック方程式に対して，その係数である電磁ポテンシャルを境界データ または内部データから決定する逆問題（係数決定逆問題）を考えた．双曲型方程式に対する 既知のカーレマン評価を用いて，境界観測をした場合と内部観測をした場合について， それぞれリプシッツ型安定性評価を得た． さらに，後者の内部観測した場合には，4成分ある観測データのうち2成分のみの観測によって ヘルダー型の安定性評価を導出した．
  2. Atsushi Kawamoto, Inverse problems for linear degenerate parabolic equations by "time-like" Carleman estimate, Journal of Inverse and Ill-posed Problems 23 (2015) 1--21.
    DOI : 10.1515/jiip-2013-0027
    柱状領域における線形退化放物型方程式に対して，部分境界上のデータとある時刻における 空間データから源泉項の時間依存因子を決定する逆問題（源泉決定逆問題）を調べた． 線形退化放物型方程式に対して重み関数が時間のみに依存するカーレマン評価を導出し， このカーレマン評価を用いて，源泉決定逆問題における一意性とリプシッツ型安定性評価を確立した． さらに，強結合型の線形退化放物型方程式系に対しても同様の結果を得た．
  3. Atsushi Kawamoto, Hölder stability estimate in an inverse source problem for a first and half order time fractional diffusion equation, Inverse Problems and Imaging 12 (2018) 315--330.
    DOI : 10.3934/ipi.2018014
    空間多次元の領域における1 階時間偏導関数と1/2 階時間偏導関数を含む複数項時間非整数階拡散方程式に対し， ある時刻での空間データから内部領域における源泉項の時間独立因子を決める逆問題（源泉決定逆問題）を調べた． 放物型方程式に対する既知のカーレマン評価から，この非整数階拡散方程式に対する局所的カーレマン評価を確立した． そして，このカーレマン評価を用い，源泉決定逆問題におけるヘルダー型安定性評価を得た．
    この論文は以下のハンドブックで引用されました：
    Anatoly N. Kochubei and Yuri Luchko (Editors), Handbook of Fractional Calculus with Applications. Volume 2, Fractional Differential Equations, Berlin: De Gruyter, 2019. [ web ]
  4. Atsushi Kawamoto, Lipschitz stability estimates in inverse source problems for a fractional diffusion equation of half order in time by Carleman estimates, Journal of Inverse and Ill-posed Problems 26 (2018) 647--672.
    DOI : 10.1515/jiip-2016-0029
    空間1次元時間1/2 階拡散方程式に対し，ある時刻における空間データの観測に加え， 境界データの観測または内部データの観測から源泉項の時間独立因子を決定する逆問題（源泉決定逆問題）の研究を行った． この方程式に対し，境界項付きカーレマン評価と内部項付きカーレマン評価を得た． これらのカーレマン評価を用いることで，境界観測と内部観測した場合の源泉決定逆問題において， それぞれリプシッツ型安定性評価を確立した．
    この論文は以下のハンドブックで引用されました：
    Anatoly N. Kochubei and Yuri Luchko (Editors), Handbook of Fractional Calculus with Applications. Volume 2, Fractional Differential Equations, Berlin: De Gruyter, 2019. [ web ]
  5. Atsushi Kawamoto and Manabu Machida, Lipschitz Stability in Inverse Source and Inverse Coefficient Problems for a First- and Half-order Time-fractional Diffusion Equation, SIAM Journal on Mathematical Analysis 52 (2020) 967--1005. (39 pages)
    DOI : 10.1137/18M1235776
    空間多次元の時間1階と1/2階の非整数階拡散方程式に対して， 源泉項の時間独立因子を決定する逆問題（源泉決定逆問題）と 拡散係数など方程式の係数を決定する逆問題（係数決定逆問題）を考えた． この方程式に対し，境界項付きカーレマン評価と内部項付きカーレマン評価を導出した． ある時刻における空間データの観測に加え，境界観測と内部観測した場合について， 源泉決定逆問題と係数決定逆問題におけるリプシッツ型安定性評価を得た．
  6. Atsushi Kawamoto and Manabu Machida, Global Lipschitz stability for a fractional inverse transport problem by Carleman estimates, Applicable Analysis 100 (2021) 752--771.
    DOI : 10.1080/00036811.2019.1620931
    異常輸送現象を記述する方程式として知られている非整数階輻射輸送方程式に対して， その物理係数である吸収係数と散乱係数の和（全減衰係数）および散乱係数を境界データなどから決定する逆問題（係数決定逆問題）を研究した． 空間1次元の場合の時間1/2階輻射輸送方程式に対して，境界項付きカーレマン評価を示した． また，このカーレマン評価を用いて，係数決定逆問題におけるリプシッツ型安定性評価を導出した．
    この論文は以下のハンドブックで引用されました：
    Anatoly N. Kochubei and Yuri Luchko (Editors), Handbook of Fractional Calculus with Applications. Volume 2, Fractional Differential Equations, Berlin: De Gruyter, 2019. [ web ]
  7. Xinchi Huang and Atsushi Kawamoto, Inverse problems for a half-order time-fractional diffusion equation in arbitrary dimension by Carleman estimates, Inverse Problems and Imaging 16 (2022) 39--67.
    DOI : 10.3934/ipi.2021040
    空間多次元時間1/2階拡散方程式を考え， 源泉決定逆問題と係数決定逆問題の研究を行った． まず，空間多次元時間1/2階拡散方程式に対して， カーレマン評価を導出した． このカーレマン評価を利用して， 任意に固定された時刻における空間データから源泉項または拡散係数の 時間独立因子を決定する逆問題におけるリプシッツ型安定性評価を確立した．
  8. Atsushi Kawamoto, Manabu Machida, Masahiro Yamamoto, Homogenization and inverse problems for fractional diffusion equations, Fractional Calculus and Applied Analysis 26 (2023) 2118--2165.
    DOI : 10.1007/s13540-023-00195-8 / SharedIt by Springer Nature
    異なる構造間における逆問題を提案した． まずはじめに，周期的構造における時間非整数階拡散方程式から均質化された構造における時間非整数階拡散方程式を均質化法によって導出した． 次に，時間非整数階拡散方程式の定数拡散係数を最小限のデータから決定する係数決定逆問題において，一意性と安定性を調べた． 最後に，異なる構造間における逆問題を考えた． ひとつは周期的構造におけるデータから均質化された構造における定数拡散係数を決定する逆問題であり， もうひとつは均質化された構造におけるデータから周期的構造における拡散係数を決定する逆問題である． そして，これらの係数決定逆問題において，一意性と安定性評価を得た．
    以下は，この論文の概念図です． ２つの赤い矢印がこの論文で新たに提案した異なる構造間における逆問題を表しています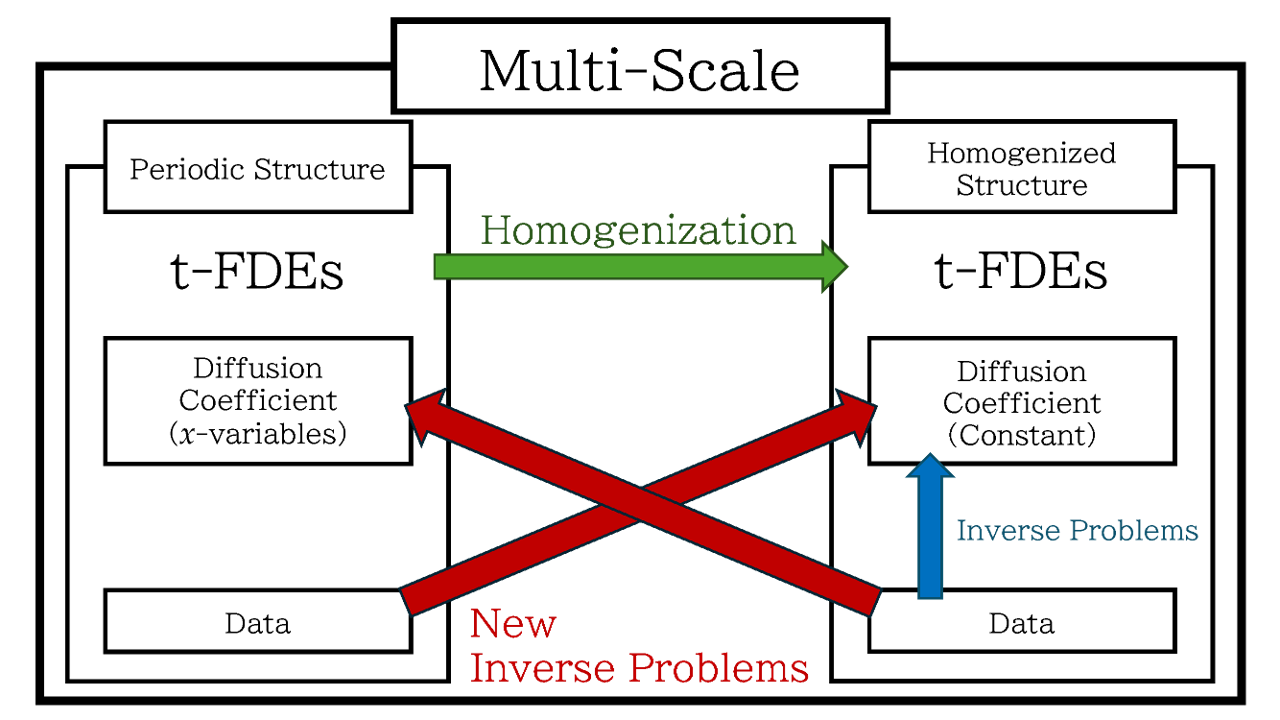． ConceptualDiagram.png

研究者 ID

ORCID :
Atsushi Kawamoto (0000-0002-1334-844X)
MR Author ID :
MR: Kawamoto, Atsushi2 - 1011186
zbMATH Author ID :
kawamoto.atsushi
Google Scholar :
Atsushi Kawamoto - Google Scholar Citations
researchmap :
川本 敦史 (Atsushi Kawamoto) - マイポータル - researchmap